Analyzing the Performance of Deep Encoder-Decoder Networks as Surrogates for a Diffusion Equation

Table of Links

Abstract and Introduction

Methods

Results

Discussion

Conclusions and References

ABSTRACT

Neural networks (NNs) have been demonstrated to be a viable alternative to traditional direct numerical evaluation algorithms, with the potential to accelerate computational time by several orders of magnitude. In the present paper we study the use of encoder-decoder convolutional neural network (CNN) algorithms as surrogates for steady-state diffusion solvers. The construction of such surrogates requires the selection of an appropriate task, network architecture, training set structure and size, loss function, and training algorithm hyperparameters. It is well known that each of these factors can have a significant impact on the performance of the resultant model. Our approach employs an encoder-decoder CNN architecture, which we posit is particularly wellsuited for this task due to its ability to effectively transform data, as opposed to merely compressing it. We systematically evaluate a range of loss functions, hyperparameters, and training set sizes. Our results indicate that increasing the size of the training set has a substantial effect on reducing performance fluctuations and overall error. Additionally, we observe that the performance of the model exhibits a logarithmic dependence on the training set size. Furthermore, we investigate the effect on model performance by using different subsets of data with varying features. Our results highlight the importance of sampling the configurational space in an optimal manner, as this can have a significant impact on the performance of the model and the required training time. In conclusion, our results suggest that training a model with a pre-determined error performance bound is not a viable approach, as it does not guarantee that edge cases with errors larger than the bound do not exist. Furthermore, as most surrogate tasks involve a high dimensional landscape, an ever increasing training set size is, in principle, needed, however it is not a practical solution.

Keywords Machine Learning · Deep Learning · Diffusion Surrogate · Encoder-decoder · Neural Networks

1 Introduction

Diffusion is ubiquitous in physical, biological and engineered systems. In mechanistic computer simulations of the dynamics of such systems, solving the steady state and time-varying diffusion equations with multiple sources and sinks is often the most computationally expensive part of the calculation, especially in cases with multiple diffusing species with diffusion constants differing by multiple orders of magnitude. In real-world problems, the number of sources and sinks, their shape, boundary fluxes and positions differ from instance to instance and may change in time. Boundary conditions may also be complicated and diffusion constants may be anisotropic or vary in space. The resulting lack of symmetry means that many high-speed implicit and frequency-domain diffusion-solver approaches do not work effectively, requiring the use of simpler but slower forward solvers [1]. Deep learning surrogates to solve either the steady-state field or the time-dependent field for a given set of sources and sinks subject to diffusion can increase the speed of such simulations by several orders of magnitude compared to the use of direct numerical solvers.

Deep learning techniques have been successfully applied to a wide range of problems by means of solving the corresponding sets of partial differential equations. This has been extensively studied in literature, with references such as [2, 3, 4, 5, 6, 7, 8]. See Ref. [9] for a thorough review. Furthermore, embedding neural networks in differential equations has also shown promising results in the area of Neural-ODEs. Modeling a physical process via an ordinary differential equation (ODE) typically involves equating the rate of change of a quantity, such as a concentration, to an operator applied to that quantity and any additional quantities, known as inhomogeneities or external fields. The ODE is then solved and compared to experimental data to validate the model or fit parameters. The operator in the ODE is traditionally chosen based on the symmetries of the physical process. However, in the case of Neural-ODEs, the operator is replaced with a neural network, which is trained by solving the Neural-ODE and comparing it to experimental data [10, 11]. Diffusion models are an example of Neural-ODEs [12]. Additionally, Physics-Informed Neural Networks (PINNs) have been proposed as a means of addressing forward and inverse problems by embedding physical information into the neural network. This can be achieved by embedding the ODE, initial conditions and boundary conditions into the loss function used to train the neural network [13]. These methods have been successful in various fields, such as computational molecular dynamics [14, 15, 16]. However, the complexity of multiscale systems, which often exhibit different characteristic length and time scales differing by orders of magnitude, in addition to the lack of symmetries, can make the solution of these systems challenging. AI-based surrogates using deep learning methods can be used to accelerate computation by replacing specific classical solvers, while preserving the interpretability of mechanistic models. In the field of multiscale modeling, AI-based surrogates can provide a computationally efficient alternative to traditional approaches such as Monte Carlo methods and molecular dynamics.

The development of effective deep neural network (NN) surrogates for diffusion-solver problems is a challenging task. This is due to several factors, such as the high dimensionality of the problem specification, which includes an arbitrary pattern of sources and sinks, varying boundary conditions for each source and sink, and spatially variable or anisotropic diffusivities. Additionally, there are a number of design decisions that must be made, such as the selection of the network architecture, the structure and size of the training set, the choice of loss function, and the selection of hyperparameters for training algorithms. Furthermore, it is essential to define accurate metrics for evaluating the task-specific performance of the trained network, as this may differ from the loss function used during training.

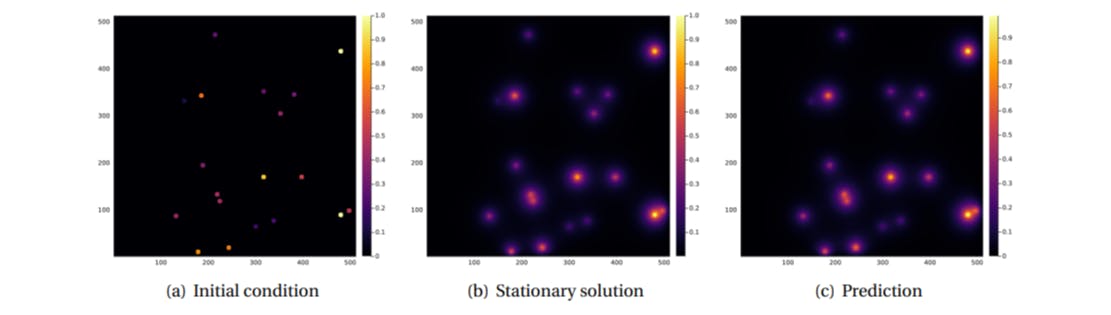
In prior work [17], we demonstrated the utility of deep convolutional neural networks in predicting the stationary solution for a diffusion problem on a 100×100 lattice with two circular random sources of radius 5 units and random fixed flux, located in random positions, under absorbing boundary conditions. Here, we extend this approach by increasing the number of sources and the lattice size to 512×512. The problem specification is as follows: we assume absorbing boundary conditions and the sources are fully contained within the domain. Each source imposes a constant value on the diffusing field within the source and at its boundary, with one of the sources having a value of 1 and the other sources having values randomly selected from a uniform distribution between (0,1] (as depicted in Figure 1(a)). Outside of the sources, the field diffuses with a constant diffusion constant (D) and linearly decays with a constant decay rate (γ). This simple geometry could represent the diffusion and uptake of oxygen in a volume of tissue between parallel blood vessels of different diameters. Although reflecting or periodic boundary conditions may better represent a portion of a larger tissue, we use the simpler absorbing boundary conditions here. The steady-state field in this case is highly dependent on the distance between the sources, the distance between the sources and the boundary, both relative to the diffusion length (lD = (D/γ) 1/2) and on the sources’ field strengths.

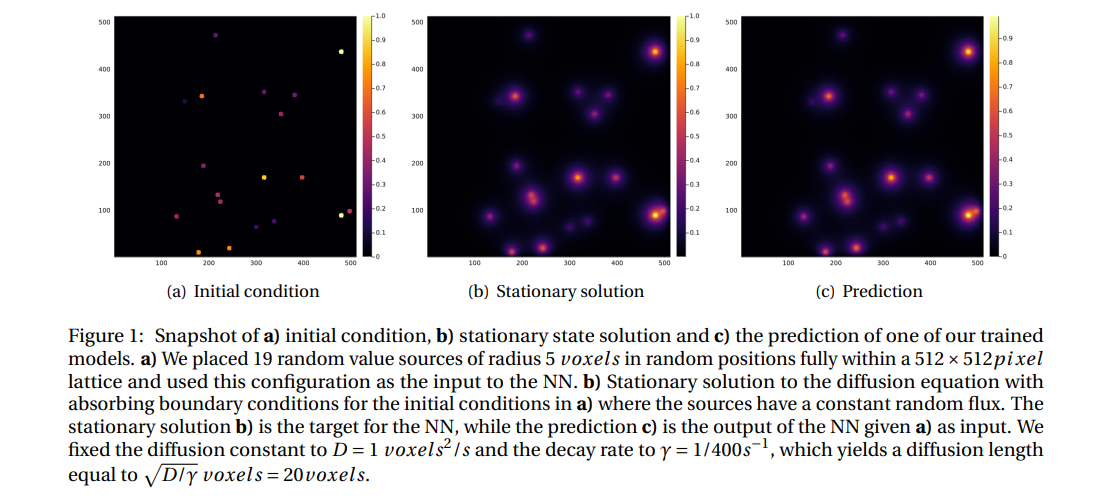
In practice, the steady-state diffusion equation maps an input image consisting of 512 × 512 pixels with a value of 0 outside the sources and constant values between 0 and 1 inside the sources, to an output image of the same size, which is a superposition of exponentially decaying functions, with its maximum at the center of each source (as illustrated in Figure 1(c)). In order to evaluate the performance of a neural network (NN) in approximating the steady-state diffusion field for configurations of sources that it had not previously encountered, we trained the NN on explicit numerical solutions of the steady-state diffusion field for 16, 000 examples per number of sources.

It is well-established that the diffusion kernel convolution used in the direct solution of the time-dependent diffusion equation, such as finite-element methods, is a type of convolutional neural network (CNN) [1]. Therefore, in our study, we chose to utilize deep convolutional neural networks (DCNNs) as the architecture. However, there are various types of CNNs that can be employed. In this study, we considered a deep convolutional neural network with the archetype of an encoder-decoder [18]. We argue that the encoder-decoder CNN architecture is particularly well-suited for this task, as it effectively transforms data, rather than compressing it, akin to the Fourier transform. Additionally, we evaluated different loss functions and prefactors to weigh in the source regions in the lattice, which are statistically undersampled in the training set. We also assessed and discussed the impact of different hyperparameters and training set sizes on the model performance.

However, in order to accurately evaluate the performance, it is essential to define a suitable metric. We discussed different metrics to evaluate the different models trained. Our results suggest that increasing the size of the training set has the most significant effect on reducing performance fluctuations and overall error. Furthermore, we studied the performance of models versus training set size and found that as the training set size increases, the performance fluctuations decrease, and the computational time for training increases linearly. In addition, the model performance has a logarithmic dependence on the training set size.

It is crucial to acknowledge that our findings do not indicate the existence of an optimal training set size. Rather, our results suggest that training a model with a pre-determined error performance bound is not a viable approach, as it does not guarantee that edge cases with errors larger than the bound do not exist. Furthermore, as most surrogate tasks involve a high dimensional landscape, an ever increasing training set size is, in principle, needed, however it is not a practical solution.