Author:
(1) Attila Losonczi.
Table of Links
1.1 Basic notions and notations
1.2 Basic definitions from [7] and [8]
2 Generalized integral
2.1 Multiplication on [0, +∞) × [−∞, +∞]
2.3 The integral of functions taking values in [0, +∞) × [0, +∞)
2.1 Multiplication on [0, +∞) × [−∞, +∞]
In order to define the integral, we will need multiplication on [0, +∞) × [0, +∞). We will use a natural way to do that, however one might argue against it, saying that that rule does not always hold for Hausdorff dimension and measure. We admit that it is true, but we could not find a better way until now, and more importantly, this method of multiplication and the resulting integral suit our later purposes completely.
We define the operation on a greater domain that we will actually need.
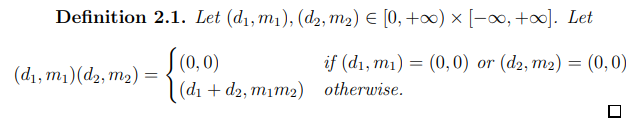
Remark 2.2. The multiplication of a real number and a value from [0, +∞) × [−∞, +∞] is a special case of the multiplication defined here, because for c ∈ R,(d, m) ∈ [0, +∞)×[−∞, +∞], we have c(d, m) = (0, c)(d, m) = (d, cm) if c 6= 0, while if c = 0, then both sides equal to (0, 0). Therefore if we identify c with (0, c), then we can embed the former algebraic structure into the current one.
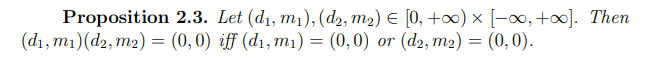
Proof. The sufficiency is obvious.
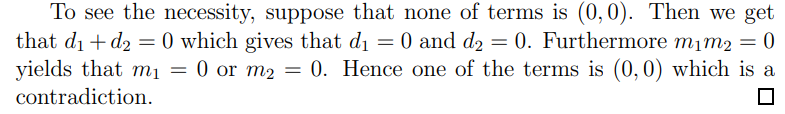
Proposition 2.4. The multiplication is commutative and associative.
Proof. Being commutative is trivial.

Proposition 2.5. The distributive law holds in [0, +∞) × [0, +∞]
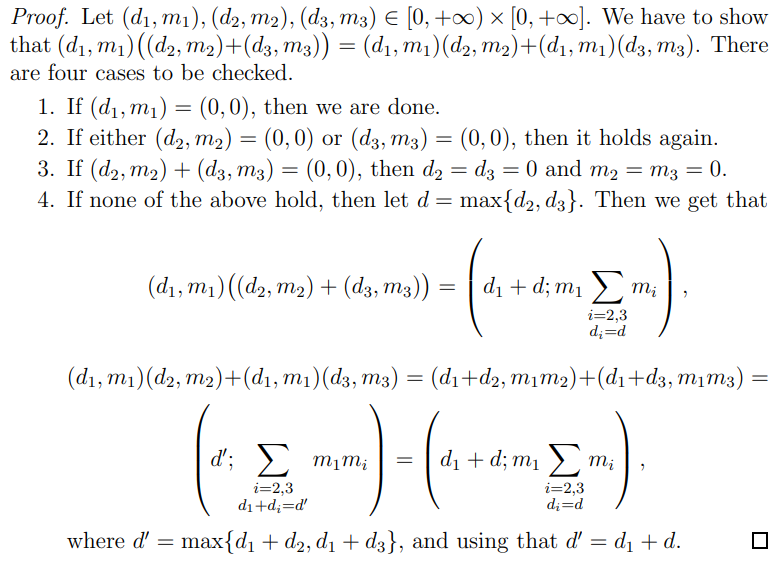
Example 2.6. The distributive law does not hold in general if we allow negative numbers in the second coordinate as well.
See e.g. (1, 1) (0, 5) + (0, −5)) = (0, 0) 6= (1, 5) + (1, −5) = (1, 0).
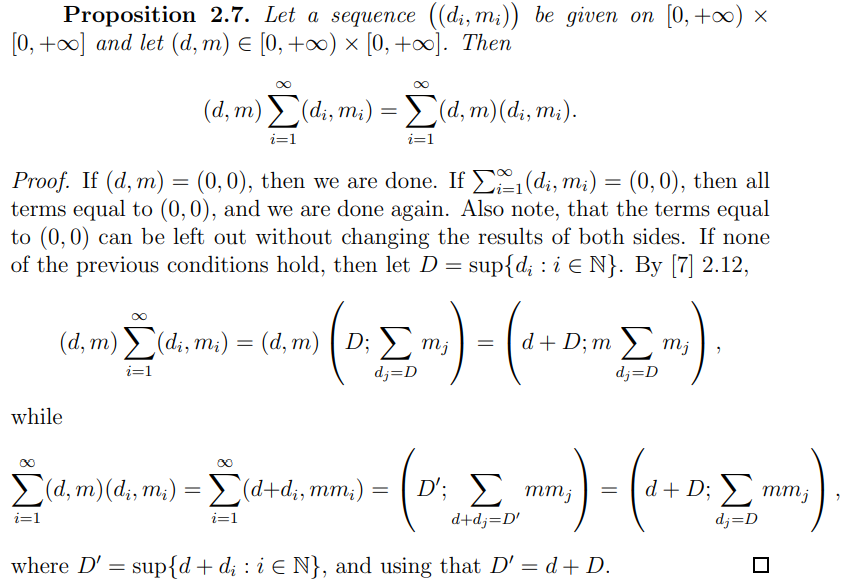

This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.