This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Z. Jennings, Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK (E-mail: [email protected]);
(2) J. Southworth, Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK;
(3) K. Pavlovski, Department of Physics, Faculty of Science, University of Zagreb, 10000 Zagreb, Croatia;
(4) T. Van Reeth, Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, B-3001 Leuven, Belgium.
Table of Links
- Abstract and Intro
- Observation
- Orbital Ephemeris
- Radial Velocity Analysis
- Spectral Analysis
- Analysis of the Light Curve
- Physical Properties
- Asteroseismic Analysis
- Discussion
- Conclusion, Data Availability, Acknowledgments, and References
- Appendix A: Ephemeris Determination
- Appendix B: Iteratively Prewhitened Frequencies
- Appendix C: Detected Tidally Perturbed Pulsations
6 ANALYSIS OF THE LIGHT CURVE
The components of KIC 9841944 are close to each other and thus have a significant tidal deformation. We therefore sought to model the light curve using a code that is based on Roche geometry. We selected the Wilson-Devinney (WD) code (Wilson & Devinney 1971; Wilson 1979) for this, and used the 2004 version of the code driven using the JKTWD wrapper (Southworth et al. 2011). The user guide which accompanies the WD code (Wilson & Van Hamme 2004) includes a description of all input and output quantities discussed below.
The WD code is computationally expensive and is not suited to the analysis of the full 500 000 short-cadence datapoints in one step. We therefore used the orbital ephemeris determined in Section 3 to convert the datapoints to orbital phase, and then binned them into a much smaller number of points. We chose a bin size of 0.001 orbital phases during the eclipses and 0.005 outside the eclipses, resulting in a total of 456 phase-binned datapoints suitable for analysis with the WD code.
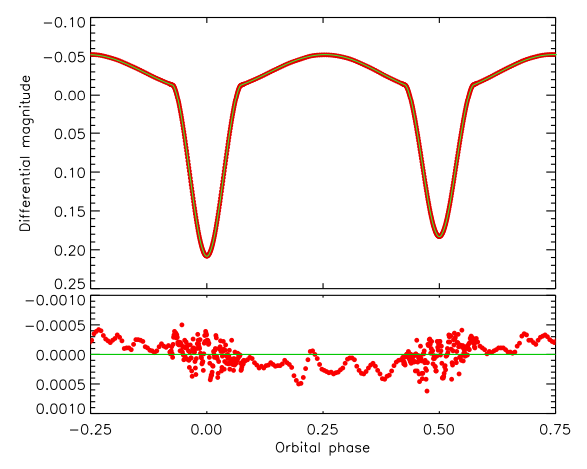
Through a process of trying a large number of different fits with a range of fixed and fitted parameters, we arrived at a good solution to the light curve. We adopt this as the default solution, plot it in Fig. 9, and give the fitted parameters in Table 6. It was obtained in Mode = 0 with the following fitted parameters: the light contributions of the two stars; their potentials; their gravity darkening coefficients; the linear coefficients of the logarithmic LD law; and the orbital inclination. We fixed the mass ratio at the spectroscopic value, the orbital eccentricity to zero, the albedos to 1.1, the logarithmic coefficients of LD to values from Van Hamme (1993), third light to zero, and the rotation rates to synchronous. We adopted the maximum numerical precision values of N1 = N2 = 60 and N1L = N2L = 60, the simple treatment of reflection, and the Cousins R-band as a proxy for the Kepler passband. This solution gives a light ratio in excellent agreement with the spectroscopic values in Table 4. The fractional radii in Table 6 are volume-equivalent values calculated by the LC component of the WD code.

For the determination of the uncertainties of the fitted parameters we ran a wide range of solutions with a large number of different possible approaches to modelling the light curve (see Southworth 2020). We calculated the errorbar for each parameter by adding in quadrature the contribution from every model choice, which in turn was taken to be the amount that parameter changed by versus the default solution. The following different approaches were explored.
(i) We varied the amount of binning prior to the WD solution, finding that it had a negligible effect on the fitted parameters.
(ii) We changed the numerical precision to N1 = N2 = N1L = N2L = 50. This modified the fractional radii by a maximum of 0.5%.
(iii) We tried the detailed reflection effect and found almost identical results.
(iv) Attempts to fit for mass ratio returned a value very close to the spectroscopic one and almost no change in the other parameters.
(v) Fitting for the rotation rates of the stars yielded values close to and consistent with synchronous rotation and little change in the other parameters.
(vi) Fitting for albedo gave a poorer fit but again very little change in the other parameters.
(vii) Allowing for third light gave very similar parameters and a very small amount of third light consistent with zero.
(viii) Fitting for one of the temperatures of the stars instead of the two light contributions directly (namely Mode = 2) changed the fractional radii by 0.2%.
(ix) Fixing the limb darkening coefficients to theoretical values changed the fractional radii by 0.5%.
(x) Using the square-root instead of logarithmic limb darkening law had a negligible effect.
The best-fitting parameters were highly robust against all these experiments. The only significantly discrepant fit (neglecting our original exploratory ones) was when we used the Cousins I-band instead of the R-band. However, we are able to reject this fit as it is not consistent with the spectroscopic light ratio. The calculated uncertainties are given in Table 6.
Fig. 9 shows that the best fit is extremely good, with an r.m.s. of 0.20 mmag, but that there are systematics remaining in the residuals. We attribute these to the WD numerical integration for points during the eclipses, and residual pulsations for points outside eclipse. Our approach of phase-binning the data gives a light curve practially without Poisson noise, so makes any imperfections in the fit easily noticable. We note that the systematics in the residuals of the fits we found to the data are too small to show up in plots of unbinned data, so may well be present in previous work on this object.

