Authors:
(1) Anatol Guglielmi, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(2) Boris Klain, Borok Geophysical Observatory of Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(3) Alexey Zavyalov, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(4) Oleg Zotov, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences and Borok Geophysical Observatory of Schmidt Institute of Physics of the Earth, Russian Academy of Sciences.
Table of Links
Discussion
We believe that the arguments in favor of the phenomenological theory of aftershocks are stronger and more convincing than the arguments in favor of the old theory based on the HiranoUtsu formula. One of the arguments in favor of a differential evolution equation containing quadratic nonlinearity is that the form of the equation suggests natural and very effective generalizations.
An obvious generalization of (2) is the inhomogeneous differential equation

The free term f (t) can be used to formally describe the triggers that induce aftershocks. Here we remember two endogenous triggers, one of which is pulsed (f (t) ∝ δ (t)), and the second sinusoidal (f (t) ∝ sin (ωt ) ). The idea is that the main shock of an earthquake excites two non-trivial triggers, namely, a round-the-world seismic echo and free vibrations of the Earth, which can affect the dynamics of the “cooling” earthquake source.
With some stretch, the theory of the two triggers we have indicated could be called semiphenomenological, since at least the echo delay time and the period of free oscillations of the Earth are calculated within the framework of the fundamental theory of elastic oscillations of the Earth. In the future, we expect that the phenomenological parameters and, above all, the source deactivation coefficient will be calculated on the basis of first principles, just as the gas temperature is calculated within the framework of kinetic theory. But the theory of aftershocks is still very, very far from such an ideal.
Generally speaking, generalization (9) is quite trivial. And it only designates exogenous and endogenous triggers, helps to classify them and the like. A nontrivial generalization of equation (2) is the logistic equation for aftershocks [23]

This equation is well known in biology, chemistry, sociology and other sciences. Here γ is the second phenomenological parameter of our theory. Its approximate estimate can be made using the formula γ σn = ∞, where n∞ is the frequency of tremors in the background seismicity regime, 𝑛𝑛∞ ≪ 𝑛𝑛0.
It should be noted that we were led to the logistic equation (9) by the research of Faraoni [24], who saw a remarkable analogy between the aftershocks equation (2) and one of Friedman’s equations, which describes the expanding Universe. Equation (9) describes the evolution of aftershocks under conditions of limited influx of free energy and negative entropy into the source. An interesting perspective opens up when considering the stochastic analogue of the logistic equation for aftershocks.
We started with the simplest nonlinear evolution equation (2), carefully substantiated its applicability for describing aftershocks, and with great care made minimal generalizations reflecting certain features of the source dynamics, while trying not to destroy the basis of our phenomenological theory. Now we want, with all the necessary reservations, to make a radical generalization and consider the source as a spatially extended object [3, 7, 14, 25]. To do this, we replace the frequency of aftershocks n (t) with the distribution density of aftershocks n (t, x), where x = (x, y, z) are the coordinates of the hypocenter. If the distribution of epicenters is analyzed, then x = (x, y) should be set and the origin of the coordinate system should be aligned with the epicenter of the main shock. Finally, sometimes the epicenters of aftershocks are located predominantly in the vicinity of a long fault in the earth's crust. In this case, a simplified description of the distribution of aftershocks using the function n (t,x) is acceptable, with the distance x measured along the fault.

Here D is the third phenomenological parameter of our theory.

Along this path, the complex task of experimentally searching for directional migration of aftershocks was formed. The problem was first successfully solved in [14] (see also [3, 25]). The difficulty is this. We want to consider the source as a kind of track detector. We will monitor the movement of aftershocks and try to estimate the velocity of movement. But we talk about the movement of aftershocks only figuratively. Each discontinuity that excites an aftershock occurs locally. In fact, the localization of the sequence of ruptures moves underground.

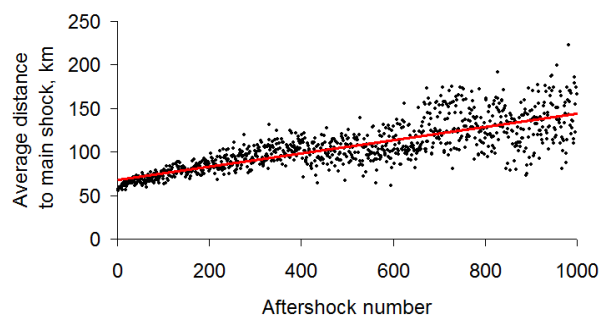
Recognizing that the flow of aftershocks moves away from the main shock is a big step toward understanding earthquake mechanics. Here the key results have not yet been obtained. We still have to learn how to calculate the flow of Umoff’s mechanical energy in the source of earthquake. We need to understand the mechanism of formation of the Umoff flow velocity in a rock mass. Intuition tells us that the divergent flow of aftershock energy may correspond to a converging flow of foreshock energy, and we still have to test this hypothesis experimentally.
So, 130 years have passed since the search for the law of aftershock evolution began. The process turned out to be complex and contradictory. And, of course, one cannot say that the process has already been completed. But we can make a number of statements quite definitely:
– the law of aftershock evolution has the form of a differential equation containing quadratic nonlinearity,
– Omori’s law is fulfilled, but has a time-limited range of applicability,
– at the end of the Omori epoch, the state of the source as a dynamic system changes sharply, which probably indicates the phenomenon of bifurcation,
– there is a slow removal of the epicenters of aftershocks from the epicenter of the main shock.
This paper is available on arxiv under CC BY 4.0 DEED license.

